Abstract

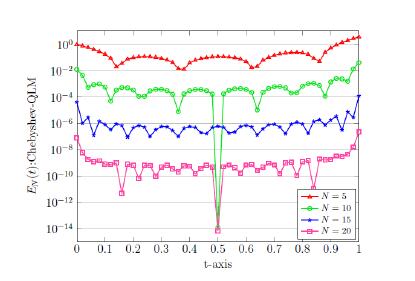
In this work, Chebyshev orthogonal polynomials are employed as basis functions in the collocation scheme to solve the nonlinear Painlevé initial value problems known as the first and second Painlevé equations. Using the collocation points, representing the solution and its fractional derivative (in the Caputo sense) in matrix forms, and the matrix operations, the proposed technique transforms a solution of the initial-value problem for the Painlevé equations into a system of nonlinear algebraic equations. To get ride of nonlinearlity, the technique of quasi-linearization is also applied, which converts the equations into a sequence of linear algebraic equations. The accuracy and efficiency of the presented methods are investigated by some test examples and a comparison has been made with some existing available numerical schemes.